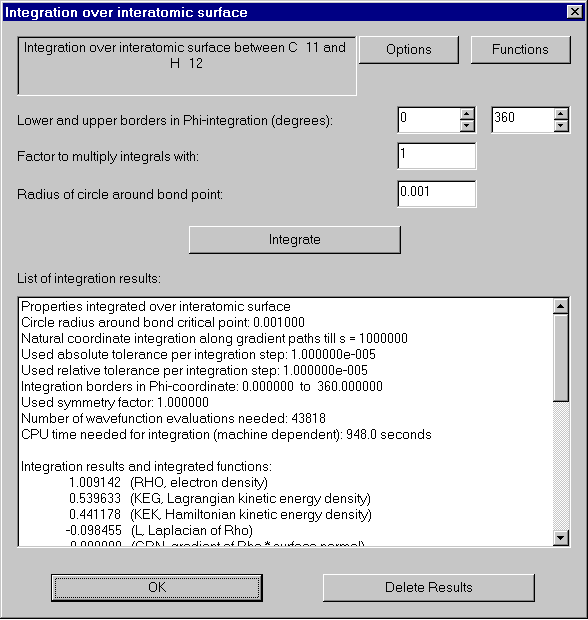
The integration over an interatomic surface computes a two-dimensional integral:
s
runs along a gradient path, Phi determines the initial direction of a
path and usually runs from 0 to 360 degrees.
The first aspect a user has to think about is the use of symmetry which can very much
accelerate the integration process. You can enter the borders of the Phi-integration
under lower and upper borders in the Phi-integration (degrees) using the
spin-buttons.
Beneath the spin-buttons, a factor is shown by which the integration results are multiplied, e.g. 2*Phi if the upper and lower border of the Phi-integration are equal (rotational symmetry) or 4 if Phi runs from 0 to 90 degrees. The program presets this factor after the integration borders are chosen, but the user can overwrite this value.
The third value the user has to enter is the radius of the circle around the (3, -1)-critical point. Inside this circle the curvature of the surface is assumed to be zero and all properties are assumed to be constant. A small sphere enhances the accuracy, but the sphere-radius must be well above the accuracy of the critical point!
Buttons of the dialog:
All results are displayed in the lower list-box of the dialog. For comments on the integrated functions and properties see Surface Properties.