Options / Basin integration options

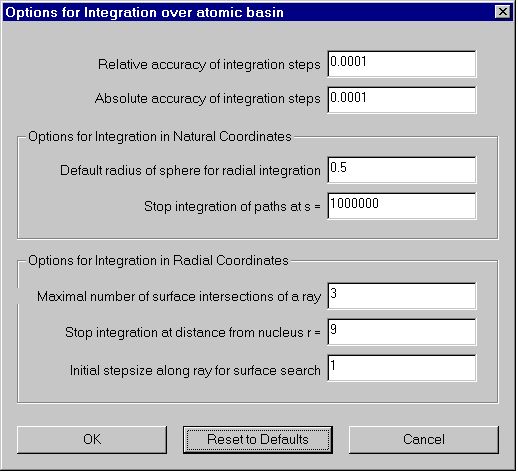
• Relative accuracy of integration steps: 1e-004.
  Required relative accuracy for each step of the differential equation solver. Caution! Decreasing this value may result in a steep increase of computer time needed!
• Absolute accuracy of integration steps: 1e-004.
  Required absolute accuracy for each step of the differential equation solver. Caution! Decreasing this value may result in a steep increase of computer time needed!
• Options for Integration in Natural Coordinates:
  • Default radius of sphere for radial integration: 0.5.
    Inside a sphere of this radius, a polar coordinate system is used for integration. The sphere must totally be contained inside the basin. This is usually the case with a value of 0.5, but especially for Hydrogen atoms, this value may be too high.
  • Stop integration of paths at s = 1000000.
    In natural coordinates, the s-variable runs along a gradient path. Its limit is always infinity. A value of 1000000 usually corresponds to a path length of 7 to 8 atomic units, where most integrated functions are neglectable. In some cases it may be useful to increase this value.
• Options for Integration in Radial Coordinates:
  • Maximal number of surface intersection of a ray: 3
    A ray in  radial coordinates is defined by the two angles Theta and Phi. It can intersect the surface of a basin several times. For the calculation of the intersection points a bisection method is employed. If you know that all rays intersect the surface at most once you can save a lot of computer time by reducing this number to 1.
  • Stop integration at distance from nucleus r=9:
    Reducing this number also saves computer time.
  • Initial step size along ray for surface search:
    Along a ray a grid with this step size is constructed. For each grid point an ...... gradient path is computed in order to decide to which basin the point belongs. Increasing this number will also increase the risk of missing 2 surface intersections of the ray. After an interval with intersection point is found, this point is computed via a bisection method.