Critical points

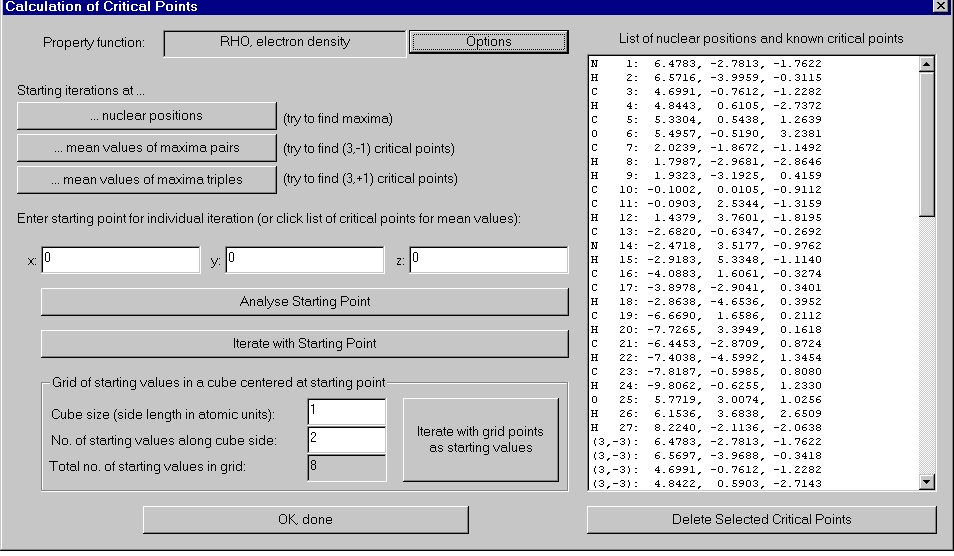
Critical points of the charge density are usually the first items you will want to compute, since the whole theory of atoms in molecules is based on their properties. Of course, critical points of other density functions can also be computed (see Control View).

At critical points all components of the gradient of the density function vanish. Apart from the gradient, the Hessian matrix of second derivatives is also available at each point (it is computed directly from the wave function or numerically).
Hence Newton's method can be employed to calculate the zeros of the gradient. Newton's method turned out to be superior to all other methods like conjugate gradient or quasi-Newton-methods. But it is heavily dependent on the choice of starting values.

AIM2000 helps you in several ways to choose starting values for a successful iteration:

• Most densities have maxima at or near the nuclear positions of the atoms in the molecule. It is therefore sensible to use nuclear positions as starting values. These starting values are tried when the button Starting iterations at nuclear positions is clicked.
• Bonds in a molecule are represented by critical points of the charge density with inertia (3, -1) which are located between two atoms. Hence the mean value of two charge density maxima is usually a good starting value. These starting values are tried when the button Starting iterations at mean values of maxima pairs is clicked. Of course, the procedure can also be used for other densities.
• Ring-critical points are often found when starting with the mean value of three charge density maxima. These starting values are tried when the button Starting iterations at mean values of maxima triples is clicked. Of course this procedure also works for others than the charge density. Caution! For molecules with many atoms this procedure may be slow!
• If none of the above procedures finds the critical point you suspect in a certain region, you can input a starting value of your own. This value can be analyzed via the analyze-button and iteration started via the Iterate with starting point-button.
  You can also compose your starting values by clicking into the list of nuclear positions and computed critical points. The composed starting point is the arithmetic mean of all highlighted entries in the list.
• Some density functions (e.g. The Laplacian density) frequently have a very high number of critical points. In order to find all critical points in a certain region, you can define a grid of starting points in a cubic region of space. The center of the cube is the preset starting point. You can set the length of a cube-side and the number of starting values along the cube-side. Notice the total number of starting points you defined! Iterate with grid points as starting values starts the iteration.

For all types of starting point choices, the program will present a record of the iterations and their success. Successfully computed critical points will be entered into the right hand side list together with their inertia.
The Options-button brings you to a dialog where you can manipulate the used Newton iteration process.

Delete selected critical points removes the highlighted critical points from the list.
OK, done closes the dialog.